Lecture 1-1 Information

학교 수업 복습 칸입니다. 25년 Fall, Pattern Recognition and Machine Learning

들어가면서.

이 수업은 패턴인식론과 생성형 알고리즘을 다루는 수업이다. 강의 순서는 다음과 같다.

1. Information
2. PCA, LDA
3. Bayesian Decision
4. Bayesian Network
5. Parametric Estimation
6. Non-parametric Estimation
7. Variational Inference
8. Deep Generative model

강의의 범위가 좀 넓은데. 일단 패턴인식론을 어디서부터 어디까지 배우는지 좀 두고 봐야 할듯하다.

1. Information

1.1 정보의 정의

정보(Information)를 어떻게 정의할 것인가. 이것이 첫번째 질문이다.

확률적 사건이 발생했을때 불확실성이 얼마나 줄어드는가
The simplest of the many definitions of information in Shannon’s theory is that information is a decrease in uncertainty
(https://cs.stanford.edu/people/eroberts/courses/soco/projects/1999-00/information-theory/information_1.html)

이산 확률 변수 X 가 있다고 하자. 교재에서는 Discrete Random variable 이라고 표현한다. 이 X가 이루는 집합을 $\Psi$ 라고 하자.

\(\Psi = \{ x_k | k = 0, \pm 1, ...., \pm K \}\) 무서워하진 말자. 그냥 사건의 집합을 표현한것이다.

이 “어떤 사건” $X = x_k$ 가 확룔 $p_k=P(X=x_k)$로 발생한다고 할때, 그 사건이 주는 정보량 $I$ 은 아래와 같이 표현할 수 있다.

\[I(x_k) = - \log p_k = \log \left( \frac{1}{p_k} \right)\]

개인적으로 중간의 마이너스 부호달린걸 좋아한다마는… 여튼 수식만 놓고 봤을때, 확율이 높은 정보($p_k \uparrow ,or \approx 1 $)는 $I$값이 0에 근접하게 된다. 별 정보가 못된다는 말이다. 반대로 확율이 낮은 정보는 그 값이 점점 커지게 된다.

<div style="text-align: center;">
 <img src="/assets/images/robotics/information_p_graph.png" alt="정보량?">
 <figcaption>Information과 확률 P의 그래프 <br> <br> </figcaption>
</div>

그래프의 y축을 유심히 보면, bit라는 단어가 보인다. 로그의 밑(base)에 따라 정보의 단위가 달라진다. Base의 선택은 쓰는 사람 마음인가 싶다. 기준이 없네.

• $\log_2$ : 비트 (bits), 컴퓨터/디지털통신에서 일반적으로 사용
• $\log_e$ : 낫 (nats) 확률/통계, 연속확률분포시 편하다고 한다.
• $\log_10$ : 하틀리, (Hartley, 또는 Hart), 전신이나 전화통신연구에서 썻다고 한다.

#### 예시)

• 동전의 앞/뒷면의 확율 : $p=0.5$ $\rightarrow$ $I = \log_2 (\frac{1}{0.5}) = \log_2 2 = 1$ bit
• 주사위의 확율 : $p=1/6$ $\rightarrow$ $I = \log_2 (6) = 2.58$ bits
• 거의 불가능한 사건 : $p=0.001$ $\rightarrow$ $I = \log_2 (10000) = 9.97$ bits

2. 엔트로피

어떤 확률변수 $X$ 의 평균적인 정보량. 즉 기대정보량을 엔트로피라고 부른다.
A measure of the average amount of information conveyed per message, i.e., expectation of information

\[H(X) = \mathbb{E}[I(X)] = \displaystyle \sum_{k=-K}^{K} p_k I(x_k) = - \displaystyle \sum_{k=-K}^{K} p_k \log p_k\]

이때 몇가지 아래와 같이 몇가지 특성을 가질 수 있다.

• 최대 엔트로피 : $p_k$가 균등한 확율(equiprobable)이면, 즉 다 같은 확율이면. 최대값을 가진다.
  (위의 엔트로피식에서는 -K~K 까지의 합으로 정의했으나, 이해의 직관성을 높이기 위해 1~n으로 바꿔 써본다. )

\[0 \leq H(X) \leq - \displaystyle \sum_{k=1}^n \frac{1}{n} \log \frac{1}{n} = -n \frac{1}{n}\log \frac{1}{n} = \log n\]

• H(X) = 0 인 경우는 $p_k$ 가 1이거나 0일때.
  즉 사건집합 $\Psi$에서 한 사건의 확율이 1이면 나머지 사건은 0이어야 한다. 집합에 있는 확율의 총 합은 1이기때문이다.
  달리 말보면, 사건의 집합에서 단 한 사건만 일어나기때문에 혼잡도는 0인것으로 해석해도 된다.

• Theorem (Gray, 1990) –> KL Divergence 는 항상 양수다. \(\sum_k p_k \log\left(\frac{p_k}{q_k}\right) \ge 0\) 이 식은 두 분포의 거리를 뜯한다.
  • KL divergence는 항상 0 이상이다.
  • 두 확률분포 (p)와 (q)가 같을 때만 0이 된다.
  • 즉, $D_{p|q} \ge 0$, equality if $p=q$.
• Relative Entropy ( or Kullback-Leibler Divergence 즉 KL divergence) \(D_{p \parallel q} = \sum_{x \in \mathcal{X}} p_X(x) \, \log \frac{p_X(x)}{q_X(x)}\)
  • $p_X(x)$: 실제 확률분포 (probability mass function, pmf)
  • $q_X(x)$: 기준(reference) 확률분포

※ KL-Divergence 의 의미
- KL divergence는 두 분포 $p$와 $q$의 차이(비대칭적 거리) 를 나타낸다.
- 값이 클수록 $q$가 $p$를 잘 근사하지 못하고 있음을 의미한다.
- 0일 때만 동일 분포임을 뜻한다.
- 비대칭성: \(D_{p \parallel q} \neq D_{q \parallel p}\) - KL divergence = 실제 분포 $p$를 따르는 데이터를 $q$라고 잘못 가정했을 때 추가로 드는 정보 비용. 따라서 모델링, 통신, 머신러닝에서 두 분포가 얼마나 다른지 평가하는 척도로 널리 사용된다.

2.1 KL Divergence 예시

조건

• 실제 분포:
  $ p = (0.5, \; 0.5) $
• 참조 분포:
  $ q = (0.9, \; 0.1) $
• 로그 밑: 2 (단위 = bits)

KL Divergence 계산

\(\begin{aligned} D_{p \parallel q} &= \sum_i p_i \log_2 \frac{p_i}{q_i} \\ &= 0.5 \log_2 \frac{0.5}{0.9} + 0.5 \log_2 \frac{0.5}{0.1} \end{aligned}\)

계산 결과: \(D_{p \parallel q} \approx 0.737 \; \text{bits}\)

해석

• 실제 분포는 균등분포지만, 이를 $q=(0.9,0.1)$라 잘못 가정하면
  평균적으로 약 0.737 비트의 추가 정보 비용이 필요하다.
• KL divergence가 0보다 크므로 두 분포는 서로 다르다.
• 값이 클수록 모델링 오차가 크다는 의미이다.

3. Mutual Information (상호 정보량, MI)

두 확률변수 $X$와 $Y$가 있을대, $X$를 알면 $Y$에 대한 불확실성이 얼마나 줄어드는지를 나타낸다.
즉, 공유하는 정보량을 말하며, “서로 얼마나 의존적인가” 를 수치로 표현한다.

• 만약 두 변수가 독립이면 $I(X;Y) = 0$.
• 완전히 종속적이면 $I(X;Y) = H(X) = H(Y)$.

\[I(X;Y) = \sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x,y) \, \log \frac{p(x,y)}{p(x)p(y)}\]

• $p(x,y)$: 결합 확률분포
• $p(x), p(y)$: 주변 확률분포
• 이는 KL Divergence의 특수한 형태라고 표현할 수 있다. \(I(X;Y) = D_{\mathrm{KL}}\left(p(x,y) \parallel p(x)p(y)\right)\)

상호정보량 I 를 나타내는 벤다이어그램

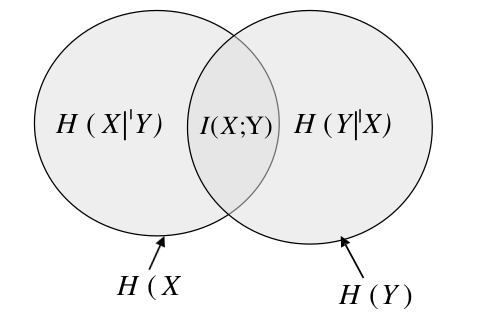
Mutual information이 왜 KL Divergence의 형태로 설명되는가에 대해 알아보기 위해 Conditional Entropy를 먼저 알아봐야 한다.

## 3.1 Conditional Entropy (조건부 불확실성의 양)

이산 확률변수의 경우:

\[H(X\mid Y) = \sum_{y} p(y)\,H(X\mid Y=y) = -\sum_{x,y} p(x,y)\,\log p(x\mid y)\]

• $H(X\mid Y)$: $Y$가 주어졌을 때 남아 있는 $X$의 평균 불확실성
  또는 $Y$가 관측되고 난 후의 $X$의 정보 기대치(Entropy)

• $Y$가 설명해주는 부분은 제외되고, 잔여 불확실성만 남음

• 위의 벤다이어그램을 다시 보자.

• Theorem (Gray, 1990) –> Chain rule
  결합 엔트로피는 조건부 엔트로피로 분해 가능하다.

  \[H(X,Y) = H(Y) + H(X\mid Y) = H(X) + H(Y\mid X)\] \[0 \le H(X\mid Y) \le H(X)\]
  • 상한: $H(X\mid Y) = H(X) - I(X;Y) \le H(X)$
  • 하한: $H(X\mid Y) \ge 0$ (이산형의 경우)
• 평등조건
  • $H(X\mid Y) = 0$: $X$가 $Y$의 함수일 때 (즉, $Y$가 $X$를 완전히 알려줌)
  • $H(X\mid Y) = H(X)$: $X$와 $Y$가 독립일 때

## 3.2 Joint Entropy (결합)

\[H(X,Y) = -\sum_{x \in X} \sum_{y \in Y} p(x,y)\log p(x, y) \\\]

$p(x,y)$: Joint probility mass funtion

3.3 Mutual Information 의 수식 유도

Mutual Information 기본 정의

Mutual Information : Output Y의 관측에 의해 알수 있는 X의 Uncertainty(정보)

\[I(X;Y) = H(X) - H(X\mid Y)\]

엔트로피 전개

체인 룰을 사용하면: $$ I(X;Y) = H(X) + H(Y) - H(X,Y) $$

각 엔트로피를 풀어쓰면:

• $H(X) = -\sum_x p(x)\log p(x)$
• $H(Y) = -\sum_y p(y)\log p(y)$
• $H(X,Y) = -\sum_x \sum_y p(x,y)\log p(x,y)$

이걸 이제 이어서 전개해보면 다음과 같다.

\[\begin{aligned} I(X;Y) &= H(X)-H(X \mid Y) \\ &= H(X) + H(Y) - H(X,Y) .............(1) \\ &= -\sum_{x \in X} p(x)\log p(x) - \sum_{y \in Y} p(y)\log p(y) + -\sum_{x \in X} \sum_{y \in Y} p(x,y)\log p(x, y) ............(2) \\ &= \sum_{x \in X} \sum_{y \in Y} p(x,y)\log p(x, y) \end{aligned}\]

(1) : 조건부 엔트로피의 정리(체인룰)을 참조할 것. 

주변분포와 결합분포 관계

주변분포는 결합분포의 합으로 표현된다: \(p(x) = \sum_{y \in Y} p(x,y), \quad p(y) = \sum_{x \in X} p(x,y)\)

• 주변분포(Marginal) : 결합분포에서 특정변수 하나만 집중할때, 나머지 변수값을 모두 합쳐서 없앤것.
  예를 들어 보자.
  X = {0,1}, Y={0,1}, 이때 p(x,y) 는 x와 y가 특정값을 가지는 확율이라고 해보자.
  X가 Y에 상관없이 0 일 확율을 알고 싶으면, p(x,y)일때, p(0,0),p(0,1)을 더하면 $p(x)|_{x=0}$ 을 구할 수 있다.
  이 개념으로 접근하면 y 값들의 누적합 $\sum$으로 표현된다.

• 수식 (2) 에서 $-\sum_{x \in X} p(x)\log p(x) $ 는 음수를 로그 안으로, 그리고 $p(x)$를 바꿔 쓰면
  $\sum_{x \in X} \sum_{y\in Y}\frac{\log p(x,y)}{\log p(x)} $ 로, 마찬가지 방식으로 p(y)도 치환할 수 있게 된다.
  
  
  
• 따라서, 이를 이용하면 모든 항을 결합분포 $p(x,y)$ 만으로 쓸 수 있다.

\[I(X;Y) = \sum_x \sum_y p(x,y) \log \frac{p(x,y)}{p(x)p(y)}\]

해석

• 마지막 형태는 KL divergence 꼴이다: \(I(X;Y) = D_{\mathrm{KL}}\big(p(x,y)\;\|\;p(x)p(y)\big)\)

4. 예제 풀이

프리미어리그에서 아스널과 토트넘이 경기를 하고 있다. TV를 보며 마음 껏 떠들 수 있도록 자리가 마련된 **치킨집의 식객 30명**과 바로 옆 삽겹살 집 식객 60명이 응원전을 펼치고 있다.

치킨집 사람들에게 어느 팀을 응원하는지 물었을 때 토트넘 10명, 아스널을 20명이 응원한다고 답했다.

삼겹살 집에서는 각 팀을 몇 명이 응원하고 있는지 확인하지 못했다

4.1 치킨집에서 토트넘을 응원한다는 답변에 담긴 정보량 (Information gain)은?

$I(x) = - \log p(x) = - \log \frac{10}{30} = \log_2 3$

4.2 치킨집의 엔트로피는?

응원의 확율은 두개가 있다. 아스널을 응원하거나($p_1$). 토트넘을 응원하거나($p_2$).

$H(X) = -\sum_{i=1}^{2} p_i(x) \log p_i(x)$

$= -(\frac{10}{30}\log\frac{10}{30} + \frac{20}{30}\log\frac{20}{30}) $

4.3 KL-Divergence 를 최소로 하는 삼겹살집의 응원비율은?

안봐도 비디오긴 하다. 확율이 동일하면 된다. 즉 삼겹살집에선 20명이 토트텀을, 40명이 아스널을 응원하면 된다.

테이블	치킨집	삼겹살집	X=x 행
토트넘	10	n명	x = 0
아스널	20	60-n 명	x = 1
Y=y열	y=0	y=1

\[n^* = \arg\min_n D_{P(X \mid Y=0) \,\|\, P(X \mid Y=1)}\] \[D_{P(X \mid Y=0)\,\|\,P(X \mid Y=1)} = \sum_x P(X = x \mid Y=0) \log \frac{P(X = x \mid Y=0)}{P(X = x \mid Y=1)}\]

\(= \frac{1}{3} \log \frac{\frac{1}{3}}{\frac{n}{60}} + \frac{2}{3} \log \frac{\frac{2}{3}}{\frac{60-n}{60}}\) 이때 위 식을 미분하여 0인 지점을 찾으면 argmin 값이다. …..와……. 그렇게 푸는거네.

4.4 두 음식점간 Mutual information은?

두 집의 확율은 사실 독립이다. 따라서, 0.

두 확율이 독립이라면, $p(x,y) = p(x|y)p(y) = p(x)p(y)$ \(\begin{aligned} I(X;Y) &= \sum_{x,y} p(x,y) \log \frac{p(x,y)}{p(x)p(y)} \\ &= \sum_{x,y} p(x|y)p(y) \log \frac{p(x|y)p(y)}{p(x)p(y)} \\ &= \sum_{x,y} p(x)p(y) \log \frac{p(x)p(y)}{p(x)p(y)} \\ \end{aligned}\)

log항의 분자와 분모가 동일하므로, log 1. 즉 0값이다.

4.5 Mutual information과 Conditional Entropy의 관계에 의해 H(X|Y를 구하라)

\[I(X;Y) = H(X) - H(X\mid Y) = 0\]

따라서,

\[H(X) = H(X\mid Y)\] \[= \sum_{x} p(x) \log p(x)\\ = -\frac{1}{3} \log \frac{1}{3} -\frac{2}{3} \log \frac{2}{3}\]

5. ICA (Independant Component Analysis 독립성분분석)

KL divergence를 알았다면, 이제 신호 소스에서 각 성분을 분석하는 기법을 알 수 있다.

5.1. 개요

• ICA는 Blind Source Separation (BSS) 문제를 해결하는 기법이다.
• 관측된 혼합 신호에서 통계적으로 독립적인 원 신호(성분)를 복원하는 것이 목표.

5.2. 기본 모델

• 독립 신호 (Independent Sources): \(U = [u_1, u_2, \dots, u_m]^T\)

• 혼합 과정 (Mixing): \(X = AU\)
  • $A$: Mixing Matrix
  • $X = [x_1, x_2, \dots, x_m]^T$: Observations
• 분리 과정 (Demixing): \(Y = WX\)
  • $W$: Demixing Matrix (찾아야 하는 것)
  • $U, X, Y$: Zero-mean signals

5.3. 목표

• 이상적으로는, \(Y = WX = WAU = DPU\)
  • $D$: Diagonal matrix (스케일 불확실성)
  • $P$: Permutation matrix (순서 불확실성)
• 즉, ICA는 독립 성분 $U$를 스케일과 순서까지 포함해 최대한 복원하는 것을 목표로 한다.

5.4. 핵심 아이디어

• PCA는 분산이 큰 방향을 찾는 반면,
  ICA는 비가우시안성 (non-Gaussianity)과 통계적 독립성을 극대화하는 방향을 찾는다.
• 보통 엔트로피 최소화, 상호정보량 최소화, 고차통계량(예: kurtosis) 등을 이용.

5.5. 응용

• 음성 신호 분리 (칵테일 파티 문제)
• 뇌파(EEG) 분석에서 잡음 제거, 성분 분리
• 이미지 처리: 패턴, 텍스처 분리
• 금융 데이터: 독립 요인 추출

---

5.6. 요약

• ICA는 관측된 혼합 신호 $X$로부터 독립적인 원 신호 $U$를 추출하는 방법.
• 모델: $X = AU$, $Y = WX \approx U$
• 본질적인 제약: 순서(permutation)와 크기(scale)는 알 수 없음.
• 핵심 문제: Demixing Matrix $W$를 어떻게 찾는가?